История состоит из событий, каждое из которых случилось в понедельник или вторник, среду или... а правда, в какой же день недели произошла Куликовская битва или был подписан Версальский мирный договор? Теперь вам, дорогой читатель, доступна формула вычисления в уме дня недели для любой даты из двух прошедших и двух будущих тысячелетий.
Алексей Ковалёв, заместитель главного редактора
Алексей Ковалёв, заместитель главного редактора
Мог ли я, студент первого курса, будущий картограф, проходя в 1989 году службу в Группе советских войск в Германии, предполагать, что самой большой радостью во время коротких перерывов между строевой подготовкой и стрельбами станет возможность уединиться, достать из кармана измятый блокнот и... погрузиться в ряды цифр и исторических дат?
А моими армейскими товарищами станут не только рядовые и сержанты, но и древнеегипетские жрецы, Юлий Цезарь, мудрейший святитель Кирилл Александрийский и хитрейший папа Григорий XIII?
Всё началось с друзей‑сослуживцев, просивших меня, «грамотного студента», вы числить, сколько же осталось «до приказа» (и, желательно, на какой день недели приходится эта желанная дата). Конечно же, просьба звучала в тот момент, когда под рукой не было ни календаря, ни даже просто листочка бумаги — все арифметические действия необходимо было производить в уме.
Вскоре «устный календарь» на ближайшие два года был освоен в совершенстве, и в следующее воскресенье я отправился в полковую библиотеку — к справочникам и энциклопедиям.
Выяснилось, что существуют формулы нахождения дня недели для исторических дат, но все они довольно громоздки и — самое печальное — не рассчитаны на устные вычисления. Постепенно, по мере изучения истории и#nbspстроения календарей, родилась собственная методика, позволяющая проводить все операции в уме и не требующая использования большого количества исходных данных в виде таблиц. Вот ею — как новогодним подарком — я и хочу поделиться с вами, дорогой читатель. Вам понадобится лишь терпение, а также навыки счёта на уровне пятого класса школы — и любой день в истории откроет свою тайну менее чем за минуту.
Числа дня и месяца
Сразу договоримся, что «дата» — это день и месяц (например, 6 мая), а «день» — это день недели (например, воскресенье).
Год состоит из 52 недель и 1 дня — в#nbspкаждом новом году одна и#nbspта же дата смещается на один день недели вперёд. Каждый четвёртый по счёту год — необычный, високосный, в такой год происходит скачок сразу на два дня (52 недели + 2 дня).
Для использования нашей методики примем за аксиомы следующие утверждения.
Первая аксиома: все даты января и февраля относятся к предыдущему году. Будем отмечать такие даты звездочкой: 22 февраля 2014 года запишем как 22 февраля 2013*года. Кстати, в Риме времен Республики новый год так и начинался (и праздновался) — именно 1 марта.
Вторая аксиома: столетие в «нашей» системе начинается 1 марта года, номер которого заканчивается на два нуля. Например, XXI век начинается 1 марта 2000 года. Этот год считаем «нулевым» годом века. Кажется, это несложно: ведь многие и так отмечали прошлый «милленниум» не в «правильном» 2001 году, а в «красивом» 2000‑м.
Далее — несколько правил записи наших вычислений.
1. Деление нацело на семь для получения остатка записываем в фигурных скобках:
{29/7} = 1 (в 29 днях — 4 полных недели и 1 день в остатке). Если число кратно семи, примем остаток равным нулю.
{28/7} = 0.
А моими армейскими товарищами станут не только рядовые и сержанты, но и древнеегипетские жрецы, Юлий Цезарь, мудрейший святитель Кирилл Александрийский и хитрейший папа Григорий XIII?
Всё началось с друзей‑сослуживцев, просивших меня, «грамотного студента», вы числить, сколько же осталось «до приказа» (и, желательно, на какой день недели приходится эта желанная дата). Конечно же, просьба звучала в тот момент, когда под рукой не было ни календаря, ни даже просто листочка бумаги — все арифметические действия необходимо было производить в уме.
Вскоре «устный календарь» на ближайшие два года был освоен в совершенстве, и в следующее воскресенье я отправился в полковую библиотеку — к справочникам и энциклопедиям.
Выяснилось, что существуют формулы нахождения дня недели для исторических дат, но все они довольно громоздки и — самое печальное — не рассчитаны на устные вычисления. Постепенно, по мере изучения истории и#nbspстроения календарей, родилась собственная методика, позволяющая проводить все операции в уме и не требующая использования большого количества исходных данных в виде таблиц. Вот ею — как новогодним подарком — я и хочу поделиться с вами, дорогой читатель. Вам понадобится лишь терпение, а также навыки счёта на уровне пятого класса школы — и любой день в истории откроет свою тайну менее чем за минуту.
Числа дня и месяца
Сразу договоримся, что «дата» — это день и месяц (например, 6 мая), а «день» — это день недели (например, воскресенье).
Год состоит из 52 недель и 1 дня — в#nbspкаждом новом году одна и#nbspта же дата смещается на один день недели вперёд. Каждый четвёртый по счёту год — необычный, високосный, в такой год происходит скачок сразу на два дня (52 недели + 2 дня).
Для использования нашей методики примем за аксиомы следующие утверждения.
Первая аксиома: все даты января и февраля относятся к предыдущему году. Будем отмечать такие даты звездочкой: 22 февраля 2014 года запишем как 22 февраля 2013*года. Кстати, в Риме времен Республики новый год так и начинался (и праздновался) — именно 1 марта.
Вторая аксиома: столетие в «нашей» системе начинается 1 марта года, номер которого заканчивается на два нуля. Например, XXI век начинается 1 марта 2000 года. Этот год считаем «нулевым» годом века. Кажется, это несложно: ведь многие и так отмечали прошлый «милленниум» не в «правильном» 2001 году, а в «красивом» 2000‑м.
Далее — несколько правил записи наших вычислений.
1. Деление нацело на семь для получения остатка записываем в фигурных скобках:
{29/7} = 1 (в 29 днях — 4 полных недели и 1 день в остатке). Если число кратно семи, примем остаток равным нулю.
{28/7} = 0.
2. Дни недели пронумеруем от 1 до 6 — от понедельника до субботы. Воскресенье — день под номером 7 (или ноль, что при делении с остатком одно и то же).
3. В сокращённой записи обозначим день месяца (дату) буквой d (от англ. date), а день недели — w (от week).
С учетом первой аксиомы получается, что 1 марта — это первый день любого года (високосного или обычного). Тогда 2 марта — второй день и т. д. А#nbspвот день, предшествующий 1 марта, станем считать «нулевым» днём года (это может быть как 28, так и 29 февраля). Допустим, что этот «нулевой» день — воскресенье (как было, например, в 2010 году). Тогда 1 марта — понедельник, 2 марта — вторник. Понедельниками в этом марте являются также 8, 15, 22 и 29 числа. Соответствующие формулы выглядят так:
3. В сокращённой записи обозначим день месяца (дату) буквой d (от англ. date), а день недели — w (от week).
С учетом первой аксиомы получается, что 1 марта — это первый день любого года (високосного или обычного). Тогда 2 марта — второй день и т. д. А#nbspвот день, предшествующий 1 марта, станем считать «нулевым» днём года (это может быть как 28, так и 29 февраля). Допустим, что этот «нулевой» день — воскресенье (как было, например, в 2010 году). Тогда 1 марта — понедельник, 2 марта — вторник. Понедельниками в этом марте являются также 8, 15, 22 и 29 числа. Соответствующие формулы выглядят так:

Тогда 31 марта — среда:

Но 31 марта — это также и «нулевой» день апреля. Из этого следует, что 1 апреля в том же 2010 году — четверг. То есть:

Число 3 нужно прибавлять ко всем дням апреля, чтобы узнать день недели для любой даты месяца. Тройка и есть число месяца для апреля 2010 года (обозначим число месяца буквой m, от англ. month). Например, 24 апреля того же 2010 года:
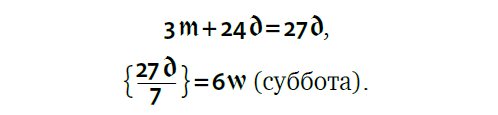
Нетрудно вычислить, что последний день апреля, 30‑е, — пятница (он же — «нулевой» день мая).

Эту пятёрку нужно прибавлять ко всем датам месяца мая, чтобы вычислить день недели. Эта пятерка и есть число мая. Таким образом, ко всем датам марта прибавляем 0 (0m);
ко всем датам апреля прибавляем 3 (3m); ко всем датам мая прибавляем 5 (5m).
Несложно вычислить числа для других месяцев, не забывая при этом, что январь* (со звёздочкой) идет после декабря (со глас но первой аксиоме). Если число получается больше 6, то удобно вычесть из него 7 — ведь это не влияет на результат!
ко всем датам апреля прибавляем 3 (3m); ко всем датам мая прибавляем 5 (5m).
Несложно вычислить числа для других месяцев, не забывая при этом, что январь* (со звёздочкой) идет после декабря (со глас но первой аксиоме). Если число получается больше 6, то удобно вычесть из него 7 — ведь это не влияет на результат!
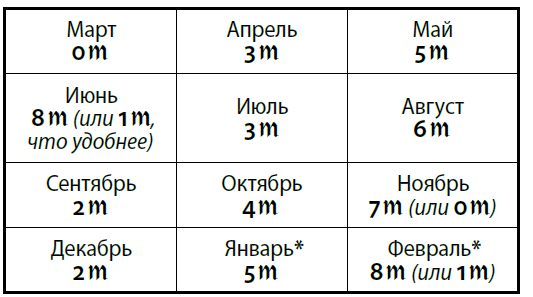
В короткой записи эта формула [1] выглядит так:

Эти цифры несложно запомнить (например, скороговоркой «ноль тридцать пять, сто тридцать шесть...»).
Несколько примеров. Текущий год по григорианскому календарю начался 1 января 2014. А вот по «нашим» правилам текущий, 2014*‑й, год начался 1 марта 2014 г. и закончится 28 февраля 2015 г. Примем, что в течение всего года «со звездочкой» действует число года 5y (от англ. year; как рассчитывается число года, рассмотрим в следующей главе).
Давайте вычислим дни недели для нескольких дат нашего 2014* года.
31 марта 2014.
Как мы помним из таблицы [1], число марта — 0m.
Несколько примеров. Текущий год по григорианскому календарю начался 1 января 2014. А вот по «нашим» правилам текущий, 2014*‑й, год начался 1 марта 2014 г. и закончится 28 февраля 2015 г. Примем, что в течение всего года «со звездочкой» действует число года 5y (от англ. year; как рассчитывается число года, рассмотрим в следующей главе).
Давайте вычислим дни недели для нескольких дат нашего 2014* года.
31 марта 2014.
Как мы помним из таблицы [1], число марта — 0m.

14 января 2015 = 14 января 2014*.
Согласно той же таблице, число января — 5m.
Согласно той же таблице, число января — 5m.
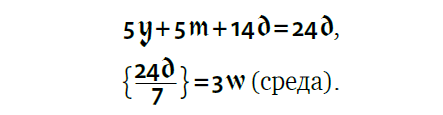
Число года
XXI век начался 1 января 2001 года. Однако мы «начнём» его 1 марта 2000 года (вторая аксиома). Эта дата приходилась на среду. Следовательно, «нулевой» день 2000 года (и, соответственно, всего XXI века) — вторник (2w) 29 февраля 2000 года (или, в нашей записи, 29 февраля 1999* года — со глас но первой аксиоме).
Вычислить дни недели на все даты 2000* года теперь не составляет труда.
24 ноября 2000 = 24 ноября 2000*.
XXI век начался 1 января 2001 года. Однако мы «начнём» его 1 марта 2000 года (вторая аксиома). Эта дата приходилась на среду. Следовательно, «нулевой» день 2000 года (и, соответственно, всего XXI века) — вторник (2w) 29 февраля 2000 года (или, в нашей записи, 29 февраля 1999* года — со глас но первой аксиоме).
Вычислить дни недели на все даты 2000* года теперь не составляет труда.
24 ноября 2000 = 24 ноября 2000*.
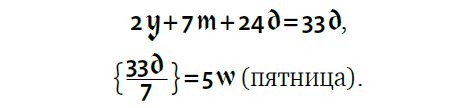
Из‑за того, что в году 52 недели и 1 день (365 дней), в следующем, 2001 году, число года увеличится на один и станет равным 3y. В 2002 году — 4y, в 2003 году — 5y.
2004 год — високосный, состоящий из 366 дней, для него «нулевой» день — не 28, а 29 февраля 2004 (он же 29 февраля 2003*). За счёт дополнительного дня число года увеличится на два — 7y (или 0y, что, конечно, то же самое).
Далее, до очередного високосного года, 2008‑го, ежегодное приращение составит также единицу. Для вычисления числа любого года была найдена эмпирическая фор мула.
Этот, пожалуй, самый сложный из этапов в нашей работе состоит из четырёх действий. Сделаем это на примере текущего 2014* года.
I. Определяем високосный год, предшествующий данному. В нашем случае — 2012* (он же — 12‑й год текущего века).
II. Делим номер високосного года на два:
12/2 = 6.
2004 год — високосный, состоящий из 366 дней, для него «нулевой» день — не 28, а 29 февраля 2004 (он же 29 февраля 2003*). За счёт дополнительного дня число года увеличится на два — 7y (или 0y, что, конечно, то же самое).
Далее, до очередного високосного года, 2008‑го, ежегодное приращение составит также единицу. Для вычисления числа любого года была найдена эмпирическая фор мула.
Этот, пожалуй, самый сложный из этапов в нашей работе состоит из четырёх действий. Сделаем это на примере текущего 2014* года.
I. Определяем високосный год, предшествующий данному. В нашем случае — 2012* (он же — 12‑й год текущего века).
II. Делим номер високосного года на два:
12/2 = 6.
III. Получившееся число вычитаем из ближайшего бóльшего, кратного семи. В#nbspнашем случае: 7 – 6 = 1.
IѴ. К этому числу прибавим разность между искомым годом и високосным годом (действие I). В данном случае — 2 (разность между 2014 и 2012). Получим: 1 + 2 = 3y.
К получившемуся числу можно прибавить число века (напоминаю, что в текущем веке это 2c, а в XX веке — 3c): 2c + 3y = 5cy. Если помнить это число 5 в течение всего 2014* года, то вычисление ближайших дат будет занимать не более нескольких секунд.
Итак, в 2014* году для расчёта дней недели с 1 марта по 28 февраля пользуемся числом года (с учётом числа века) 5сy.
Например, вычислим день недели для 25 мая 1970 года.
IѴ. К этому числу прибавим разность между искомым годом и високосным годом (действие I). В данном случае — 2 (разность между 2014 и 2012). Получим: 1 + 2 = 3y.
К получившемуся числу можно прибавить число века (напоминаю, что в текущем веке это 2c, а в XX веке — 3c): 2c + 3y = 5cy. Если помнить это число 5 в течение всего 2014* года, то вычисление ближайших дат будет занимать не более нескольких секунд.
Итак, в 2014* году для расчёта дней недели с 1 марта по 28 февраля пользуемся числом года (с учётом числа века) 5сy.
Например, вычислим день недели для 25 мая 1970 года.
1. Число века. С 1 марта 1900 по 29 февраля 2000 (или, в нашей записи, по 29 февраля 1999*) это число 3c (от англ. century — столетие; формула для вычисления числа века дана в следующей главе).
2. Число года. Ближайший предшествовавший високосный год — 1968‑й.
68/2 = 34.
Ближайшее кратное семи, бÓльшее, чем 34, число — 35. Получаем:
2. Число года. Ближайший предшествовавший високосный год — 1968‑й.
68/2 = 34.
Ближайшее кратное семи, бÓльшее, чем 34, число — 35. Получаем:
35 – 34 = 1.
Прибавляем два (70 – 68 = 2). Итак, чис ло года: 1 + 2 = 3y.
3. Число месяца мая — 5m (см. таб лицу [1]).
4. Дата — 25d.
5. Складываем все найденные числа:
Прибавляем два (70 – 68 = 2). Итак, чис ло года: 1 + 2 = 3y.
3. Число месяца мая — 5m (см. таб лицу [1]).
4. Дата — 25d.
5. Складываем все найденные числа:

6. Находим остаток от деления на 7:
{36 d/7} = 1 w (понедельник).
Остаётся добавить, что для первого, второго и третьего года любого столетия достаточно к числу века прибавить лишь разницу между текущим годом и «нулевым». Например, для 1902* года это: 2 + 3 = 5y (второй год + число века 3). Для «нулевого» года любого века число года равно числу века (для 1900* года это 3y).
{36 d/7} = 1 w (понедельник).
Остаётся добавить, что для первого, второго и третьего года любого столетия достаточно к числу века прибавить лишь разницу между текущим годом и «нулевым». Например, для 1902* года это: 2 + 3 = 5y (второй год + число века 3). Для «нулевого» года любого века число года равно числу века (для 1900* года это 3y).
Число века для григорианского календаря
Все вычисления выше справедливы для григорианского календаря, то есть мы рассчитывали дни недели для дат по новому стилю. Следует отметить, что наш метод подходит и для юлианского (старый стиль), и для ново юлиан ско го календарей, но с небольшими уточнениями (об этом — в следующем номере журнала «Мир музея»).
Как же устроено столетие в григорианском календаре?
Век = 36 524 дня
(365 дней × 100 лет + 24 високосных дня).
24 дополнительных дня — это двадцать девятые февраля високосных лет. Висо кос ным является каждый четвертый по счету год, за исключением оканчивающихся на два нуля (1900 или 1800 год — не висо кос ные). Именно поэтому двадцать девятые февраля встречаются в «обычном» столетии только 24, а не 25 раз.
Однако каждое четвёртое по счёту столетие содержит не 24, а 25 високосных лет. Таким, например, является ушедший XX век. В эти столетия годы, оканчивающиеся на два нуля, являются високосными и включают 29 февраля. Эти годы — 1600, 2000, 2400, 2800 и так далее (их номер должен быть кратным 400). Назовём такой век «длинным», в#nbspпротивоположность «обычному».
«Длинный» век = 36 525 дней
(365 дней × 100 лет + 25 високосных дней).
«Длинными» веками были XѴI и XX. Такими могли бы стать также XII, ѴIII и IѴ века (1200, 800 и 400 годы), но григорианский календарь (новый стиль) был введён в ряде стран буллой папы Григория XIII «Среди важнейших задач...» лишь в 1582 году. За три века он стал обще миро вым, а до этого человечество пользовалось юлианским календарем (даты по старому стилю).
36 524 дней «обычного» века — это 5217 недель и 5 дней. Если бы суток было на двое больше, то каждый век начинался бы с одного и того же дня недели. А так — начало каждого сто летия «отступает» на два дня по отношению к предыдущему.
Как мы уже знаем, число XX века — 3c. Соответственно, число XIX века — 5c, XѴIII века — 7c, а XѴII века — 9c (последнее число удобнее записать как 2c, что при делении с остатком то же самое).
В «длинном» веке 5217 недель и 6 дней. Таким образом, следующий за ним век «отступает» от «длинного» лишь на один день. Именно поэтому число XXI века — 2w (пос ле 3w для предыдущего, XX века).
За 400‑летний цикл, состоящий из трёх «обычных» и одного «длинного» века, любая дата одного и того же года перемещается ровно на одну неделю:
3 века × 2 дня + 1 век × 1 день = 7 дней.
Ниже дана таблица чисел века для вычисления дат григорианского календаря [2].
Все вычисления выше справедливы для григорианского календаря, то есть мы рассчитывали дни недели для дат по новому стилю. Следует отметить, что наш метод подходит и для юлианского (старый стиль), и для ново юлиан ско го календарей, но с небольшими уточнениями (об этом — в следующем номере журнала «Мир музея»).
Как же устроено столетие в григорианском календаре?
Век = 36 524 дня
(365 дней × 100 лет + 24 високосных дня).
24 дополнительных дня — это двадцать девятые февраля високосных лет. Висо кос ным является каждый четвертый по счету год, за исключением оканчивающихся на два нуля (1900 или 1800 год — не висо кос ные). Именно поэтому двадцать девятые февраля встречаются в «обычном» столетии только 24, а не 25 раз.
Однако каждое четвёртое по счёту столетие содержит не 24, а 25 високосных лет. Таким, например, является ушедший XX век. В эти столетия годы, оканчивающиеся на два нуля, являются високосными и включают 29 февраля. Эти годы — 1600, 2000, 2400, 2800 и так далее (их номер должен быть кратным 400). Назовём такой век «длинным», в#nbspпротивоположность «обычному».
«Длинный» век = 36 525 дней
(365 дней × 100 лет + 25 високосных дней).
«Длинными» веками были XѴI и XX. Такими могли бы стать также XII, ѴIII и IѴ века (1200, 800 и 400 годы), но григорианский календарь (новый стиль) был введён в ряде стран буллой папы Григория XIII «Среди важнейших задач...» лишь в 1582 году. За три века он стал обще миро вым, а до этого человечество пользовалось юлианским календарем (даты по старому стилю).
36 524 дней «обычного» века — это 5217 недель и 5 дней. Если бы суток было на двое больше, то каждый век начинался бы с одного и того же дня недели. А так — начало каждого сто летия «отступает» на два дня по отношению к предыдущему.
Как мы уже знаем, число XX века — 3c. Соответственно, число XIX века — 5c, XѴIII века — 7c, а XѴII века — 9c (последнее число удобнее записать как 2c, что при делении с остатком то же самое).
В «длинном» веке 5217 недель и 6 дней. Таким образом, следующий за ним век «отступает» от «длинного» лишь на один день. Именно поэтому число XXI века — 2w (пос ле 3w для предыдущего, XX века).
За 400‑летний цикл, состоящий из трёх «обычных» и одного «длинного» века, любая дата одного и того же года перемещается ровно на одну неделю:
3 века × 2 дня + 1 век × 1 день = 7 дней.
Ниже дана таблица чисел века для вычисления дат григорианского календаря [2].

Если номер века делится на четыре, то число века — 3c. Далее по порядку — 2 – 7 – 5. Именно так — «три – два – семь – пять» — таблицу легко запомнить.
Напомним, что григорианский календарь используется с 15 октября 1582 года. Кстати, каким днём недели была эта дата?
15 октября 1582.
1. Число века. До 29 февраля 1600 года (или, вернее, до 29 февраля 1599*) это чис ло 3c — см. таблицу [2].
2. Число года. Ближайший висо кос ный год — 1580‑й.
80/2 = 40.
Ближайшее бÓльшее, кратное семи, число — 42. Имеем: 42 – 40 = 2.
К этой двойке прибавляем ещё два (82 – 80). Итак, число года: 2 + 2 = 4y.
3. Число месяца для октября — 4m.
4. День месяца — 15d.
5. Складываем все эти числа:
Напомним, что григорианский календарь используется с 15 октября 1582 года. Кстати, каким днём недели была эта дата?
15 октября 1582.
1. Число века. До 29 февраля 1600 года (или, вернее, до 29 февраля 1599*) это чис ло 3c — см. таблицу [2].
2. Число года. Ближайший висо кос ный год — 1580‑й.
80/2 = 40.
Ближайшее бÓльшее, кратное семи, число — 42. Имеем: 42 – 40 = 2.
К этой двойке прибавляем ещё два (82 – 80). Итак, число года: 2 + 2 = 4y.
3. Число месяца для октября — 4m.
4. День месяца — 15d.
5. Складываем все эти числа:

6. Находим остаток от деления на 7:
{26 d/7} = 5w (пятница).
В следующем номере мы рассмотрим работу с датами юлианского календаря, а также соответствие дат старого и нового стилей.
Увлекательных задач вам в новом году, дорогие коллеги!
Продолжение см:
Ковалёв А. 1000000 дней нашей эры // Мир музея. 2015. №2. С. 54 – 55.
Ковалёв А. 1000000 дней нашей эры // Мир музея. 2015. №4. С. 50 – 52.
{26 d/7} = 5w (пятница).
В следующем номере мы рассмотрим работу с датами юлианского календаря, а также соответствие дат старого и нового стилей.
Увлекательных задач вам в новом году, дорогие коллеги!
Продолжение см:
Ковалёв А. 1000000 дней нашей эры // Мир музея. 2015. №2. С. 54 – 55.
Ковалёв А. 1000000 дней нашей эры // Мир музея. 2015. №4. С. 50 – 52.
[1] А вот, например, по китайскому календарю начало текущего года пришлось на 31 января.
[2] Годы, начинающиеся 1#nbspмарта и#nbspзаканчивающиеся 28 (одна звёздочка) или 29 (две звёздочки) февраля.
[2] Годы, начинающиеся 1#nbspмарта и#nbspзаканчивающиеся 28 (одна звёздочка) или 29 (две звёздочки) февраля.
Печатается по: Ковалёв А. 1000000 дней нашей эры // Мир Музея. 2014. №12. С. 53 – 54.
На илл.: Папа римский Григорий XIII и математик и астроном Христофор Клавий обсуждают реформу календаря.
На илл.: Папа римский Григорий XIII и математик и астроном Христофор Клавий обсуждают реформу календаря.
